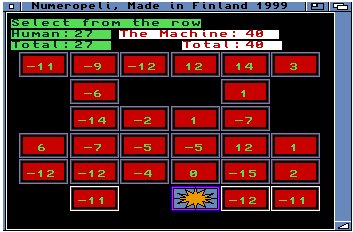
Nyt on hyvä peli! Älkää jättäkö sitä kokeilematta aikaisempien kokemustenne perusteella "peleistäni".
Yli kymmenen vuoden tauon jälkeen päätin ryhtyä käyttämään Pascal-ohjelmointikieltä. Voi miksi olen yrittänytkään koskaan käyttää mitään muuta? Se on Amigalla helppoa ja halpaa PCQ-freeware-kääntäjällä - sen jälkeen kun systeemin saannut asetettua ja sitä on oppinut käyttämään... tai no jaa, melkoista pilkunviilausta se ohjelmointi aina on. Pascal oli hallitseva opetuskieli yliopistomaailmassa 70- ja vielä pitkälti 80-luvulla. Pascalin syntaksissa kaikki muuttujat ja tyypit on esiteltävä lohkojen (ts. ohjelmien tai aliohjelmien) alussa, mikä aluksi saattaa tuntua hankalalta mutta kuitenkin helpottaa ohjelmointia ja karsii huolimattomuusvirheitä, kun ne eivät mene edes kääntäjästä läpi... tai niiden ei pitäisi; vaikuttaa siltä, että esimerkiksi Integer- ja Real-tyyppisiä muuttujia saa PCQ:ssa käyttää samoissa lausekkeissa, jolloin saattaa tulla virheitä, kun Real-luvun tallennus tulkitaan Integeriksi.
Pascal suosii - ellei peräti vaadi - rakenteellista ohjelmointia, jossa ohjelmoitava ongelma on jaettu selkeisiin aliohjelmiin. Se muistuttaa paljolti C-kieltä. Kuten yleensäkin ohjelmointikielillä, silläkin voi tehdä tietysti vaikka mitä. Eroja on lähinnä syntaksin pilkkusäännöissä.
Sillä on tullut suoritettua perus- ja aineopintojen labroja - suoritettua, muttei palautettua. Olin niin kypsynyt yliopiston arvomaailmaan, jossa tärkeintä oli kerätä suorituspisteitä kopioimalla laskuharjoituksia, että menin toiseen äärimmäisyyteen: opiskelin omaksi huvikseni ja tiedokseni ja jätin merkkaamatta laskuharjoitukset ja palauttamatta labrat. Helvettiäkö minun ohjelmointiharrastukseni muille kuului?
Ohjelmat-hakemistosta löytyvän numeropeli-ohjelman eräs versio tuli kuitenkin aikoinaan palautettua "Tietorakenteet"-kurssiin kuuluvana harjoitustyönä, joskus vuonna 1987, silloin kun vielä uskalsin kuvitella osaavani ohjelmoida. Siinä harjoiteltiin pelipuun käsittelyä. Pelipuu on tietorakenne, johon rakennetaan kustakin pelitilanteesta vaihtoehtoiset jatkotilanteet ja valitaan paras mahdollinen siirto. Pelilaudan tilannetta kuvaa arvofunktio, joka on pelipuun solmun arvo. Koko pelilaudan tilannetta ei siis tallenneta solmun arvoksi, vaan vain arvofunktion arvo. Pelipuuta rakennettaessa täytyy pelilaudan tilannekin olla kuitenkin selvillä, jotta sitä päästään rakentamaan. Siksi pelipuun solmuun tallennetaan myös tehdyn siirron sarake- tai rivi-indeksi.
Numeropelin idea on yksinkertainen: pelaajat nostavat vuorotellen numeroituja laattoja, toinen rivittäin, siltä riviltä, jolta toinen (sarakkeittain pelaava) oli poistanut laatan. Viimeksi poistetun laatan paikalle siirretään tähtilaatta. Laattojen numerot lasketaan yhteen. Suuremman summan kerännyt on voittanut tilanteessa, jossa vuorossa oleva ei pääse enää jatkamaan, kun laatat ovat loppuneet. Tähän peliin liittyvä pelitilannetta kuvaava arvofunktio, jonka pelipuualgoritmi tarvitsee, on siis äärimmäisen yksinkertainen: kerättyjen laattojen summasta vähennetään vastustajan keräämien laattojen summa.

Alkuperäinen versio kaukaisilta opiskeluajoiltani tulosti merkkigrafiikkaa käskyrivi-ikkunaan, josta alla huvin vuoksi esimerkkiajon alkua ja loppua. Kone aloitti poistamalla täydeltä pelilaudalta laatan riviltä 3 sarakkeelta 2.
8.H1:OHJELMOINTI/pcq12d> omat/numeropeli
JOS HALUAT MUUTTAA JONKIN ALLAOLEVAN ASETUKSEN ARVOA, NIIN SYOTA VASTAAVA NUMERO 1..7.
SYOTA 8 KUN HALUAT LOPETTAA KOKO OHJELMAN TAI
SYOTA 0 KUN OLET VALMIS PELAAMAAN.
SYOTA LUKU 0..8 ?
0
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | 1| -1| 0| -8| | 2| | -1| -8| 7| -1| | 3| | 7| -5| 6| 0| | 4| | 4| 1| -7| 4| | PELITILANNE: KONE=0 PELAAJA=0 |
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | 1| -1| 0| -8| | 2| | -1| -8| *| -1| | 3| | 7| -5| 6| 0| | 4| | 4| 1| -7| 4| | PELITILANNE: KONE=7 PELAAJA=0 |
SYOTA POISTETTAVAN LAATAN SARAKEINDEKSI VALILTA 1..4:
3
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | 1| -1| 0| -8| | 2| | -1| -8| | -1| | 3| | 7| -5| *| 0| | 4| | 4| 1| -7| 4| | PELITILANNE: KONE=7 PELAAJA=6 |
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | 1| -1| 0| -8| | 2| | -1| -8| | -1| | 3| | *| -5| | 0| | 4| | 4| 1| -7| 4| | PELITILANNE: KONE=14 PELAAJA=6 |
SYOTA POISTETTAVAN LAATAN SARAKEINDEKSI VALILTA 1..4:
4
..jne. jne...
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | 1| | | *| | 2| | -1| | | | | 3| | | | | | | 4| | | | | | | PELITILANNE: KONE=13 PELAAJA=-14 |
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | *| | | | | 2| | -1| | | | | 3| | | | | | | 4| | | | | | | PELITILANNE: KONE=14 PELAAJA=-14 |
SYOTA POISTETTAVAN LAATAN SARAKEINDEKSI VALILTA 1..4:
2
| SARAKE= RIVI 1 2 3 4 | | | | | | | | 1| | | | | | | 2| | *| | | | | 3| | | | | | | 4| | | | | | | PELITILANNE: KONE=14 PELAAJA=-15 |
KONE EI VOI TEHDA ENAA SIIRTOA.
HAVISIT TALLA KERTAA.
Vaikka peli on yksinkertainen - tai juuri sen takia - on se ihmiselle kuitenkin sen verran vaikeaa, etten ole Amigaani kertaakaan voittanut vähänkään isommilla vaikeustasoilla. Tosin en jaksakaan yleensä miettiä kuin korkeintaan kaksi siirtoa eteenpäin - yleensä näpäytän hiirellä sitä rivin suurinta laattaa.
Kuinka kone sitten tarkemmin ottaen tekee siirtonsa? Samalla tavalla kuin ihminen yrittää miettiä: jos nostan tuon laatan, niin se nostaa tuon laatan, jolloin minun on nostettava jokin noista, jolloin kone pääsee kuitenkin nostamaan tuon laatan jne...
Pelipuuhun rakennetaan osoitinmuuttujilla solmut ja linkit tietty määrä siirtoja eteenpäin. Solmun arvona on siis arvofunktion arvo (=KONE-PELAAJA). Jos pelilaudan koko on vaikkapa 10x10 ruudukko, nousee solmujen määrä äkkiä melko suureksi. Kuusi tasoa eteenpäin tutkittaessa lukumäärä lähestyy miljoonaa. Tästä johtuen ei algoritmissa suinkaan rakenneta koko puuta, vaan yksi haara kerrallaan, eli solmuja tarvitaan vain kuusi kerrallaan. Tilantarve on siis kokoluokkaa 6x solmun koko, mutta koska kaikki solmut käydään läpi, on ajan tarve maksimissaan (ts. pelin alussa) luokkaa 10^6 (lopussa lähenee ykköstä, kun siirtoja ei voi enää tehdä).
Mitä sitten, kun pelipuu on saatu rakennettua? (Pee-lipuu on raa-ken-nettu, peelii on joo ovella, nuumeeria riipustettu ompi laudan ruuduille - ei kun joulu meni jo?) Kuinka Amiga valitsee siirtonsa? Olisiko houkuttelevinta valita se siirto, jota pitkin pääsee alimman tason solmuun, jossa arvofunktion arvo on suurin? Ei, sillä koneella on vastassa älykäs ihminen, joka myös haluaisi päästä solmuun, jossa arvofunktion arvo on pelaajalle edullisin.
Algoritmi purkaa pelipuuta alhaalta ylöspäin ja nostaa alemmalta tasolta parhaimman siirron ylemmälle tasolle. Se on siis vuorotellen arvofunktion suurin ja pienin arvo, koska joka toisen siirron tekee kone ja joka toisen ihminen. Lopulta kone valitsee sen siirron, jota kuvaavaan solmuun on nostettu suurin arvo.
Vaikka alkuperäisessä versiossa oli suurin osa muuttujista ohjelman ajoaikana muutettavissa, ei tässä Amiga-versiossa pääse niitä muuttamaan. Pelilaudan koko pysyy siis 6x6:ssa ja tasoja tutkitaan kahdeksan eteenpäin. En ole vielä oikein saanut rakenneltua gadtools-juttuja... Muuten ohjelma moniajaa nätisti. On siinä valikotkin. Ja ennen kaikkea ikkunan kokoa voi vapaasti muuttaa ajon aikana.
Kirjoittajan kotisivu löytyy osoitteesta http://www.mbnet.fi/~keckman.